Medida de la resistencia de puesta a tierra
Introducción:
El sistema de tierra es un elemento esencial para el sistema eléctrico de seguridad y es necesario para:
• Permitir la activación de los dispositivos de protección cuando hay un defecto de aislamiento eléctrico.
• Ecualizar el potencial de las piezas conductoras que se puede acceder de manera simultánea, con el potencial de la tierra circundante, a fin de evitar que las personas sean expuestas a voltajes peligrosos.
• Permitir que el rayo de energía se disipe en condiciones de seguridad.
• Reducir las interferencias electromagnéticas.
Debido al hecho de que se trata de un sistema diseñado para garantizar la seguridad, su eficacia debería ser verificada. La difusión del valor de resistencia es el parámetro más relevante para poner a prueba un sistema de suelo de calidad y la capacidad para llevar a cabo su función. Sin embargo, la correcta medición de este parámetro necesita cumplir varios requisitos, que serán analizados en este documento.
Naturaleza física de la resistencia de la tierra:
La comprensión de la tierra, la resistencia física natural nos ayudará a evaluar las condiciones que deben cumplirse para obtener una correcta medición.
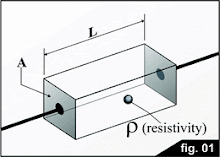
Según su definición, las resistencias de dos terminales y su resistencia se define como el cociente de la tensión aplicada sobre los terminales y la circulación actual entre ellos como consecuencia de esa tensión. El valor de la resistencia (Eq.1 Ecuación 1) (R=p.L/A) depende del tipo de material (resistividad) y sus dimensiones físicas (superficie y longitud de la resistencia).
Como se muestra a continuación:
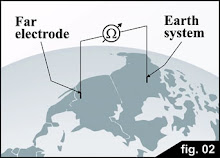
Sólo uno de los terminales es evidente en la resistencia de la tierra. Con el fin de encontrar el segundo terminal se debe recurrir a su definición: la Resistencia de la Tierra es la resistencia que existe entre la electricidad accesible por un electrodo enterrado y otro punto de la tierra, que está muy lejos, como se muestra en la grafica siguiente:
La idea es que alrededor del volumen de la tierra cerca de un electrodo enterrado, a través de una corriente inyectada, todo el planeta es el volumen equipotencial relacionado con la corriente. Cualquier punto de volumen equipotencial puede ser considerado como el segundo electrodo de la resistencia de tierra.
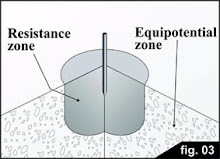
Así se ve gráficamente:
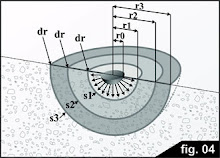
Con el fin de justificar la declaración anterior, vamos a analizar geométricamente la resistencia en la zona del electrodo enterrado que, en el siguiente ejemplo, se supone es semiesférica:
La corriente que se inyecta en la tierra a través de los electrodos enterrados sale en todas direcciones, con una densidad uniforme (suponiendo que el terreno sea homogéneo eléctricamente), y posteriormente debe pasar a través de las distintas capas que se ilustran en la figura anterior. Cada capa ofrece una resistencia al paso actual, que es proporcional a la resistividad del terreno y la capa de espesor (longitud de la resistencia en la ( Figura 1), e, inversamente proporcional a la capa de la zona, de acuerdo con eq.1. A continuación, la resistencia total es la suma de muchas pequeñas resistencias en serie. El espesor se define arbitrariamente como lo suficientemente delgado como para examinar tanto las superficies de la capa de la misma zona (requisito necesario para aplicar eq. 1).
Realmente, el espesor es infinitesimal y la suma de las resistencias es un integrante como se indica en la eq. 2, donde r0 es el radio del hemisferio enterrado.
Con el fin de permitir una más fácil visualización física del fenómeno, nos podemos imaginar la estructura de una cebolla, formada por un gran número de capas muy delgadas, cada una de las cuales representa una de las resistencias de la serie.
El concepto importante que se observa es que, desde el terreno de resistividad se suponía que iba a ser homogénea y el espesor de las capas es el mismo, el único elemento que se modifica (aumenta), a medida que desaparece el electrodo de la superficie, es de la capa. En la figura 4, se puede observar que la superficie S3 es mucho más grande que la superficie S1. Cuando la superficie aumenta, la resistencia disminuye en la misma proporción y, por tanto, la contribución hecha por las capas remotas a la resistencia total tiende a ser insignificante.
Cálculos de un electrodo hemisférico muestran que en la región más cercana, a una distancia equivalente a 10 veces el radio del electrodo, en el 90% del total se concentra la resistencia. En otras palabras, la resistencia de las capas situadas fuera de este ámbito no es significativa. Y como no hay resistencia, no hay caída de potencial. Bien. En consecuencia, fuera de la región más cercana al electrodo (llamado zona de resistencia), toda la tierra está en el mismo potencial.
Método de medición:
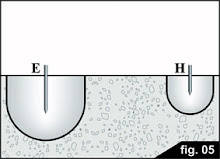
Con el fin de medir la resistencia de puesta a tierra, tenemos que aplicar un voltaje entre sus terminales que provoca la circulación de una corriente a través de él. Uno de los terminales es el sistema de acceso a tierra en contacto con E. La segunda, de acuerdo con la definición, es cualquier otro punto de la tierra, que realmente está muy lejos de la primera. Con el fin de llevar a cabo la medición, debemos clavar un electrodo auxiliar H en ese punto. El segundo electrodo tendrá inevitablemente su propia tierra, la resistencia y la zona de resistencia.
Si nos fijamos en esta grafica, veremos qué:
1. Nuestro objetivo es medir la resistencia de la tierra del electrodo E. Sin embargo, si una resistencia de medición convencional entre los puntos E y H se lleva a cabo mediante la medición de la tensión y la corriente circulante, se obtiene la suma de la resistencia de la tierra de ambos electrodos y no la resistencia de tierra del electrodo E. La diferencia puede ser muy importante puesto que, debido a su propia condición de auxiliar de electrodos, las dimensiones de H son muy pequeñas en comparación con E, por lo que su contribución a la resistencia total puede ser muy importante y la probabilidad de un error es considerable.
2. El concepto de "lejos", utilizado anteriormente sin hacer más precisiones, es ahora aclarado. De hecho, se puede considerar que el electrodo auxiliar H está lo suficientemente lejos del sistema de resistencia de la tierra que se mide cuando sus respectivas zonas de resistencia no se solapan. En tal caso, todo el volumen que queda fuera de las zonas de resistencia está, muy aproximadamente, en el mismo potencial, lo que hace posible el desarrollo del siguiente método de medición.
Método de Caída de Potencial
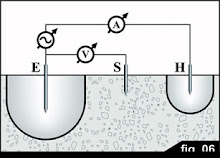
Un tercer electrodo S se utiliza con el fin de evitar el error introducido por la resistencia de tierra del electrodo de H, la vara S se ubicó en cualquier punto fuera de las zonas de influencia de E y H, dando como resultado una geometría similar a la mostrada en esta figura:
Este acuerdo se conoce como caída de Potencial y el método es el más comúnmente utilizado para la medición de la resistencia de la tierra, en la que la separación de las zonas de resistencia se obtiene con un grado razonable de distancias entre los electrodos. La corriente circula a través del sistema terrestre E y el electrodo auxiliar H, y la tensión se mide entre E y el tercer electrodo S. Esta tensión es la caída de potencial que la corriente de prueba produce en la resistencia del sistema terrestre, Rx, que en esta forma se puede medir sin ser afectada por la tierra, la resistencia de la varilla H.
La regla 62%
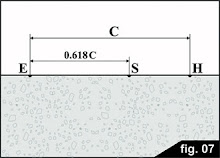
Muchas publicaciones que hacen referencia al Método de caída de potencial indican que, con el fin de obtener una medida correcta, los tres electrodos deben estar bien alineados y la distancia entre E y S debe ser el 61,8% de la distancia entre E y H. Este concepto proviene de un cuidadoso desarrollo matemático para el caso particular de un electrodo hemisférico.
Como en esta grafica se muestra:
Sin embargo, esta configuración no es fácil de aplicar en la vida real. El primer problema al que se enfrenta es que la geometría de la tierra real es compleja y difícil de asimilar con un hemisferio con el fin de determinar con precisión su centro, a partir del cual las distancias se pueden medir con precisión suficiente. Además, en las zonas urbanas es difícil encontrar lugares donde colocar las barras, y es raro que haya lugares disponibles que coincidan en su posición con los requisitos de la regla del 62% (en relación a la alineación y las distancias).
Afortunadamente, usando los mismos cálculos del método anterior podemos derivar otra geometría, que es más fácil de aplicar. Considere la posibilidad de unir E y H con la línea recta que cruza ese segmento en su punto medio y que es perpendicular al segmento mencionado. Al colocar el electrodo en cualquier punto de la línea recta los valores medidos de la resistencia se sitúan entre 0,85 y 0,95 del valor real de la resistencia de la tierra del electrodo. Luego, multiplicando el valor medido por 1,11 de la resistencia a tierra correcta se obtiene el valor, con un error inferior a ± 5%. También se observó que a medida que el voltaje del electrodo se aleja del segmento de EH, la zona en la que el valor medido se encuentra dentro del rango indicado de la tolerancia pasa a ser más amplio, con lo que el método pasa a ser más tolerante a los cambios en la posición de la tensión en el electrodo.
Tal vez el error de la propuesta pueda parecer demasiado alto. Con el fin de evaluar este punto, vamos a citar al Dr Tagg: "... tengamos en cuenta que no es necesario un alto grado de precisión. Errores de 5-10% [en la medición de la resistencia a tierra] se pueden tolerar ... Esto se debe a que una resistencia de tierra puede variar con los cambios de clima o temperatura, y, ya que tales cambios pueden ser considerables, no tiene sentido esforzarse en conseguir mucha precision."
Equipos de medicion de resistencia de puesta a tierra
• Los telurometros MRU-100/MRU-101 son equipos portátiles que miden la resistencia de puesta a tierra y la resistividad por el método de Wenner.
• El instrumento puede medir resistencia y resistividad con 2, 3 ó 4 electrodos.
• El equipo puede alimentarse con pilas estándar tipo C o con baterías.
• Las medidas pueden simplificarse usando pinzas de corriente.
Condiciones normales de operación:
• Corrientes erráticas durante la medida AC+DC: max. 24V.
• Corriente de prueba: max. 225mA.
• Medida de tensión: max. 40V.
• Frecuencia de la corriente de prueba: 128Hz.
• Temperatura de trabajo: 0..40°C.
• Tensión de alimentación (para recargar la batería): 230V.
jueves, 18 de marzo de 2010
Suscribirse a:
Enviar comentarios (Atom)

No hay comentarios:
Publicar un comentario